What the f*ck is Bresenham's Circle Drawing Algorithm?
One of the most efficient and easiest to drive of the circle algorithms is due to Bresenham.
It is not easy to display a continuous smooth arc on the computer screen as our computer screen is made of pixels organized in matrix form. So, to draw a circle on a computer screen we should always choose the nearest pixels from a printed pixel so as they could form an arc.
One of the most efficient and easiest to drive of the circle algorithms is due to Bresenham. To begin, note that only one octant of the circle need be generated. The other parts can be obtained by successive reflections. If the first octant ( 0 to 45 ccw ) is generated, the second octant can be obtained by reflection through the line y=x to yield the first quadrant. The results in the first quadrant are reflected through the line x=0 to obtain those in the second quadrant.
Much like the Midpoint Circle Drawing Algorithm, given the center point and radius of circle, Bresenham's Circle Drawing Algorithm attempts to generate the points of one octant.
Well... we already said what is given, so let us look at all of the steps of this algorithm.
✨ Step One
Given-
Centre point of Circle = (X0, Y0)
Radius of Circle = R
✨ Step Two
Assign the starting point coordinates (X0, Y0) as-
X0 = 0
Y0 = R
✨ Step Three
Calculate the value of initial decision parameter P0 as-
P0 = 3 – 2R
✨ Step Four
Suppose the current point is (Xk, Yk) and the next point is (Xk+1, Yk+1).
Find the next point of the first octant depending on the value of decision parameter Pk.
Follow the below two cases-
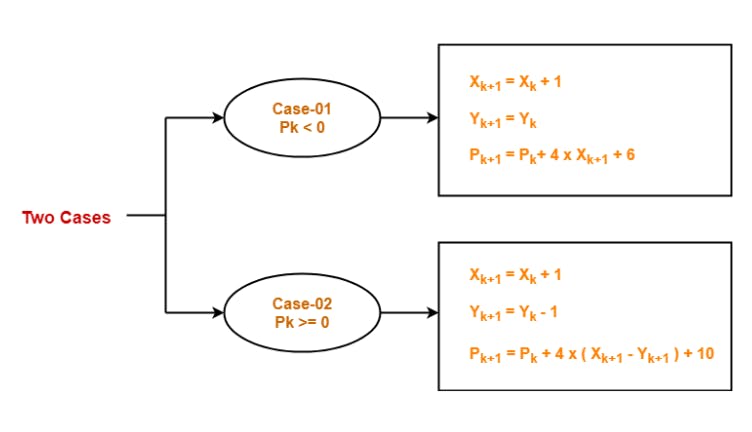
✨ Step Five
If the given centre point (X0, Y0) is not (0, 0), then do the following and plot the point-
Xplot = Xc + X0
Yplot = Yc + Y0
Here, (Xc, Yc) denotes the current value of X and Y coordinates.
✨ Step Six
Keep repeating Step-03 and Step-04 until Xplot => Yplot.
✨ Step Seven
Step-05 generates all the points for one octant. To find the points for other seven octants, follow the eight symmetry property of circle.
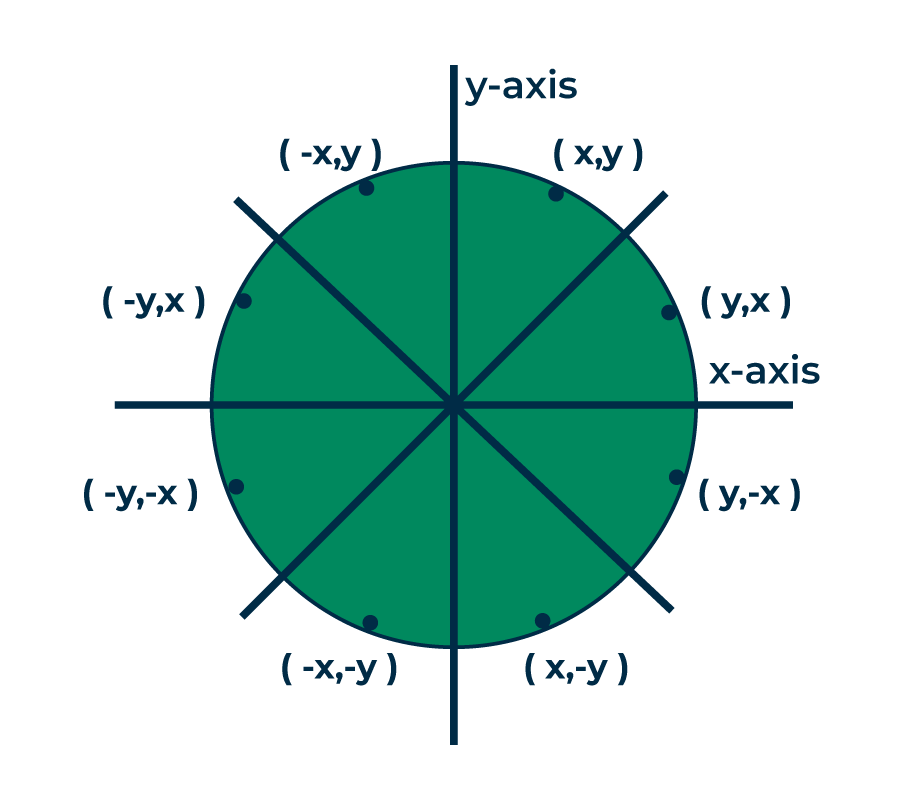
This algorithm is better than the mid point circle generating algorithm in the following terms:
It is a simple algorithm.
It can be implemented easily
It is totally based on the equation of circle i.e. x2 +y2 =r2
However, it does have some limitations:
There is a problem of accuracy while generating points.
This algorithm is not suitable for complex and high graphic images.
✨ Solved Example
Given the centre point coordinates (0, 0) and radius as 8, generate all the points to form a circle.
Given-
Centre Coordinates of Circle (X0, Y0) = (0, 0)
Radius of Circle = 8
Step One: Assign the starting point coordinates (X0, Y0) as-
X0 = 0
Y0 = R = 8
Step Two: Calculate the value of initial decision parameter P0 as-
P0 = 3 – 2 x R
P0 = 3 – 2 x 8
P0 = -13
Step Three: As Pinitial < 0, so case-01 is satisfied.
Thus,
Xk+1 = Xk + 1 = 0 + 1 = 1
Yk+1 = Yk = 8
Pk+1 \= Pk + 4 x Xk+1 + 6 = -13 + (4 x 1) + 6 = -3
Step Four: This step is not applicable here as the given centre point coordinates is (0, 0).
Step Five: Step-03 is executed similarly until Xk+1 >= Yk+1 as follows-
| Pk | Pk+1 | (Xk+1, Yk+1) |
| (0, 8) | ||
| -13 | -3 | (1, 8) |
| -3 | 11 | (2, 8) |
| 11 | 5 | (3, 7) |
| 5 | 7 | (4, 6) |
| 7 | (5, 5) |
Algorithm calculates all the points of octant-1 and terminates.
Now, the points of octant-2 are obtained using the mirror effect by swapping X and Y coordinates.
| Octant-1 Points | Octant-2 Points |
| (0, 8) | (5, 5) |
| (1, 8) | (6, 4) |
| (2, 8) | (7, 3) |
| (3, 7) | (8, 2) |
| (4, 6) | (8, 1) |
| (5, 5) | (8, 0) |
Now, the points for rest of the part are generated by following the signs of other quadrants.
The other points can also be generated by calculating each octant separately. Here, all the points have been generated with respect to quadrant-1-
| Quadrant-1 (X,Y) | Quadrant-2 (-X,Y) | Quadrant-3 (-X,-Y) | Quadrant-4 (X,-Y) |
| (0, 8) | (0, 8) | (0, -8) | (0, -8) |
| (1, 8) | (-1, 8) | (-1, -8) | (1, -8) |
| (2, 8) | (-2, 8) | (-2, -8) | (2, -8) |
| (3, 7) | (-3, 7) | (-3, -7) | (3, -7) |
| (4, 6) | (-4, 6) | (-4, -6) | (4, -6) |
| (5, 5) | (-5, 5) | (-5, -5) | (5, -5) |
| (6, 4) | (-6, 4) | (-6, -4) | (6, -4) |
| (7, 3) | (-7, 3) | (-7, -3) | (7, -3) |
| (8, 2) | (-8, 2) | (-8, -2) | (8, -2) |
| (8, 1) | (-8, 1) | (-8, -1) | (8, -1) |
| (8, 0) | (-8, 0) | (-8, 0) | (8, 0) |
This was all about Bresenham's Circle Drawing Algorithm and we finished it in style.
